
Purrrabolas
Purrrabolas
An Interactive Learning Experience
Context
The lesson described below is an example from a more extensive, interactive math product known as TenMarks Labs. These learning experiences center around an applet that allows students to explore and manipulate digital models that in-turn, expose students to the underlying mechanisms of a specific math concept.
My Role
I worked with a team of other writers, editors, and visual designers to bring the content to life. My influence on this lesson was that I came up with the context and storyboard for the learning experience, and wrote the teacher guidance documentation that accompanies the learning.
What are Math Labs?
TenMarks Labs are inquiry-based learning modules that help students make sense of math through experimentation, observation, self-explanation, and discourse. Students work with an interactive tool that allows for trial and error as they continue to refine their understanding of the concept in focus. Designed to jumpstart the learning of a particular concept or provide an opportunity to explore a concept differently, Labs promote discovery.
Lesson in Focus: Purrrabolas
Learning Objectives
1. the height of an object over time can be modeled by a parabolic curve.
2. The key features of a graph provide information about the real-world situation that it models.
Overview
The Purrrabolas lab was designed to help students understand and interpret graphs and how the features of the graph can be "read" to make sense of the real-world scenario that the graph represents.
Key Elements of Learning
01: Purposefully Engage Misconceptions
A powerful learning moment can be created when you intentionally lead students towards their own misconceptions, and then surprise them by showing them the error of their ways later down the line.
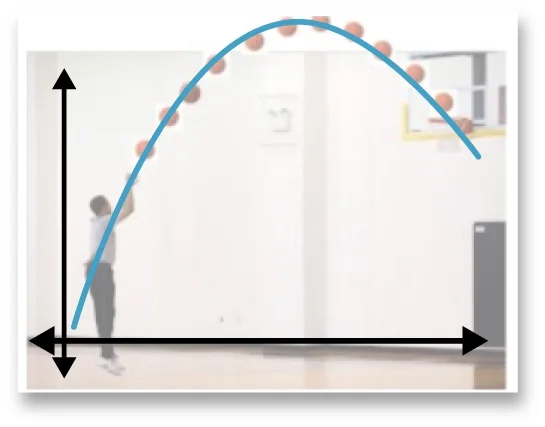
Parabolas model this type of motion, but they also model vertical motion where there is no change in the horizontal position.
Students often confuse the shape of the graph with the shape of a real-world motion. Even though all parabolas look similar, the real-world behavior that is represented in the shape can differ dramatically.
Notably, students tend to overgeneralize and think that a graph of a parabola means that an object was thrown left to right because that's the shape of the graph.
We wanted students to learn that the graph isn't a 1:1 replica of the motion in real life and that they would have to investigate the features of the graph to understand the story that it tells you.
02: Pairing a "world-view" with a "math-view"

Students can control the playback of the animation, while simultaneously looking at what happens to the graph as a result.
To help students contextualize the graph with the real-world scenario, we paired a "world-view" animation with a "math-view" animation so that students could interpret information, simultaneously, from both channels.
Including of the "world-view" gives students a low entry-point, something that they can understand and relate to. Therefore when the math-view is included, students already have some basic understandings of the variables in play and how they are behaving with respect to each other. In this case, the two variables were height and time.
03: Because CATS!
As a writing team, we already knew what the main arc of instruction was going to be, but we couldn't come up with the example. We wanted the example to be continuous throughout the lab, and in order to hit the misconception the model needed to move horizontally as well as vertically.
Then, one night, while asleep, inspiration struck me in the form of an 8-pound cat jumping with a thud down onto my bed from the tall armoire across the room. In that instant, it hit me - CATS! Cats are capable of the horizontal jumps I was looking for, but they were also possible of jumping straight up into the air when frightened enough.
This choice brought some humor to the learning.
04: Strategic Scaffolding

Since this is a discovery-based exploration, scaffolding the learning experience is crucial to guiding the students towards the intended discoveries of the lesson. To ensure that we hit the essential learnings, I storyboarded the lesson and decided on a specific sequence. With each new screen, the student received slightly new information, and as such, the learning builds upon itself one screen at a time.
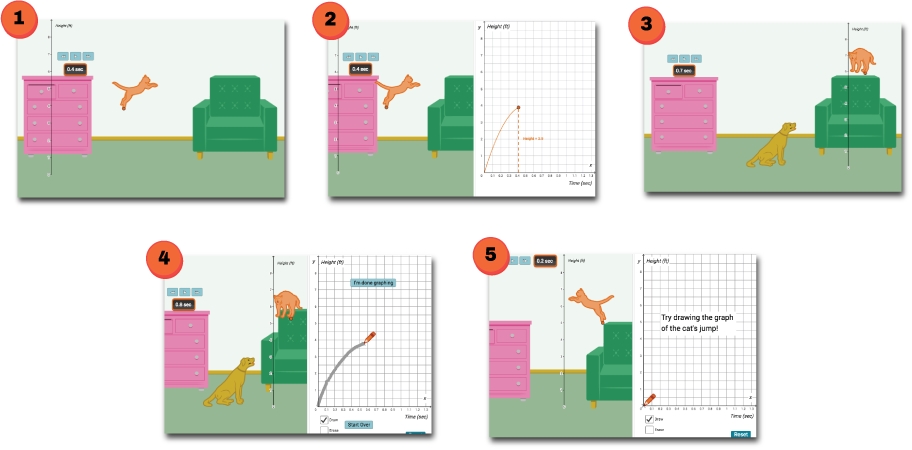
1. Students watch an animation of a cat jumping horizontally. 2. Students control the animation, while simultaneously seeing a graph drawn for them. 3. Student watches a similar, but tweaked, animation where the cat's behavior changes. 4. Now the graph isn't autogenerated; students watch animation again and sketch graph. 5. Student is given different animations, and they sketch the appropriate graph.
05: Flip the Script
The lesson had been taught by having students look at the real-world action and then look at the math. At the end of the lesson, we flipped the script by providing the graph first and then the students had to manipulate the "world-view" to create a behavior that matches the features of the graph.
06: Debriefing with Dialogue
Math Labs weren't intended to get the student to the point of mastery, they were designed only to introduce a portion of the concept. Therefore the learning needed to be concretized for the student after the experience. This occurred during an orchestrated discussion. Creating the Teacher Guidance doc was the final step.